Welcome to binney’s documentation!¶
binney is a package for doing binomial regression
(including logistic regression) with b-splines! See below
for installation instructions.
Installation¶
You can install binney with pip:
pip install binney
You will also need to install ipopt, which is an interior
point optimizer, with conda.
conda install -c conda-forge cyipopt
You can check to see if your installation worked correctly with pytest.
# pip install pytest
cd binney
pytest
Documentation¶
For instructions on how to use binney, see the API reference
for binney.run.run.BinneyRun.
Quick Start¶
Here is a quick introduction to simulate data
and do a BinneyRun. Please refer to
binney.run.run.BinneyRun for documentation on
its arguments and methods.
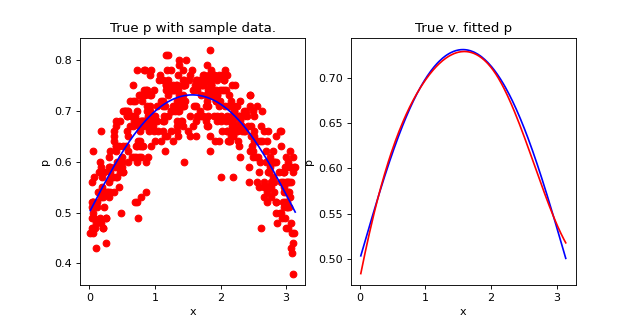
We will simulate 500 observations from
where \(p(x) = \frac{e^{sin(x)}}{1 + e^{sin(x)}}\). First, let’s create the data frame representing this simulation.
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from binney.run.run import BinneyRun
np.random.seed(0)
n = 500
x = np.random.uniform(low=0, high=np.pi, size=n)
p = np.exp(np.sin(x)) / (1 + np.exp(np.sin(x)))
df = pd.DataFrame({
'success': np.random.binomial(n=100, size=len(p), p=p),
'total': np.repeat(100, repeats=len(p)),
'p': p,
'x': x
})
df.sort_values('x', inplace=True)
df['p_hat'] = df['success'] / df['total']
Now, we can create the specifications for a binomial regression
model with binney. If you wanted to include a shape
constraint on the spline, you would do so in the splines
specifications below. See binney.run.run.BinneyRun
for more details on these specs and documentation
about all of the arguments to the function.
splines = {
'x': {
'degree': 3,
'knots_num': 4,
'knots_type': 'frequency',
}
}
b_run = BinneyRun(
col_success='success',
col_total='total',
df=df,
splines=splines,
solver_method='scipy',
data_type='binomial'
)
We can fit the model and create predictions from it.
b_run.fit()
predictions = b_run.predict()
(Source code, png, hires.png, pdf)
You can then create uncertainty as well by doing:
b_run.make_uncertainty(n_boots=50)
draws = b_run.predict_draws(df=df)